目录

深入浅出通信原理Python代码版

深入浅出通信原理是陈爱军的心血之作，于连载，此处仅作python代码笔记训练所用

陈老师的连载从多项式乘法讲起，一步一步引出卷积、傅立叶级数展开、旋转向量、三维频谱、IQ调制、数字调制等一系列通信原理知识

码元(Symbol)详解

码元，对应英文Symbol，又称符号

维基百科：持续一段固定时间的通信信道有效状态就是码元

陈老师解释：在通信信道中持续固定时间，具有一定相位或者幅值的一段余弦载波

网友：在信道(空中或电缆中）码元或者符号就是持续一定（某个）时间，具有一定（某个）幅度和一定（某个）相位的正弦波。

BPSK码元有2种(0,\(\pi\))，QPSK码元有4种，16QAM有16种码元。

设某数字调制对应码元有N种，则每个码元承载的比特数有\(log_2N\)个

但调制效率愈高，抗干扰能力愈差，对信道质量要求愈高

码元速率，也就是波特率，单位是Baud，其实就是每秒钟传输多少的码元，进一步的说，波特率是码元周期的倒数。

BPSK旋转向量理解

详见连载44-46

旋转向量在实轴上的投影就是BPSK调制后的信号，初始相位是0或者pi，但最后相位不一定落在相位0或者pi上

接收到的是个实信号，但可以分解成两者旋转向量之和：

\[ s(t)=\cos\omega_0t=Re\{e^{j\omega_0t} \}=\frac{1}{2}(e^{jw_0t}+e^{-jw_0t}) \]

此时乘上初始位置在实轴，顺时针旋转且旋转角速度是w0的单位旋转向量\(e^{-jw_0t}\)

\[ 2s(t)e^{-jw_0t}=1+2e^{-jw_0t} \]

通过低通滤波器或积分器便解调出1，即发送端发送的是-1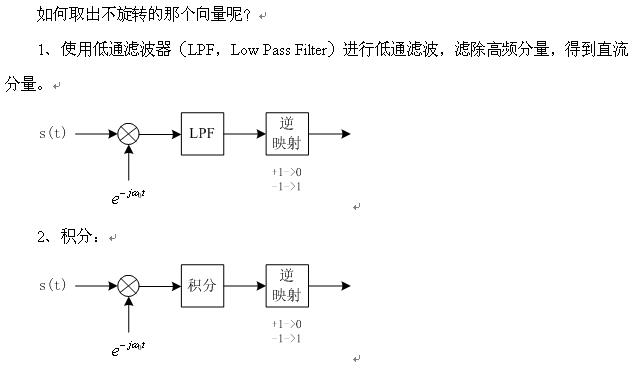

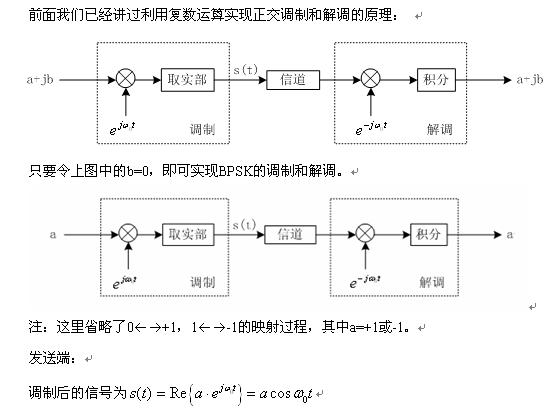
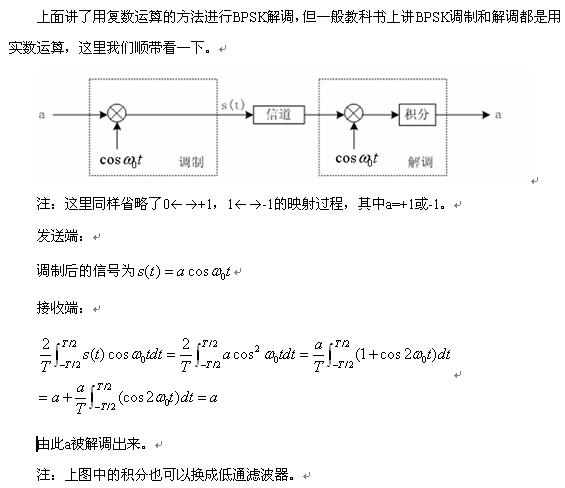
PSK=映射+调制

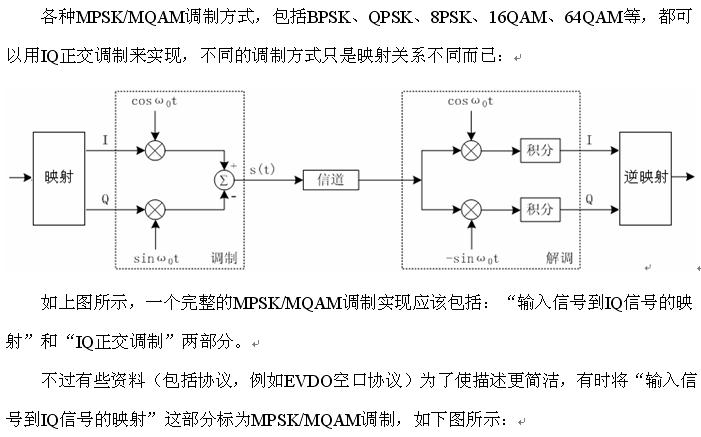
调制解调与傅里叶级数展开

IQ调制实际就是将数据作为傅里叶系数与正、余弦信号相乘后合成发送的过程

IQ解调即求解傅里叶级数的过程

\[ s(t)=a\cos(w_0t)-bsin(w_0t) \]

\[ Fourier \ \ Transform: f(t)=\frac{a_0}{2}+\sum_{k=1}^{\infty}(a_kcoskw_0t+b_ksinkw_0t)\ \]

矩形波的复傅立叶级数

周期方波信号的傅里叶级数 \(c_k=\frac{1}{2}\frac{sin(k\omega_0T_0/4)}{k\omega_0T_0/4}=\frac{1}{2}\frac{sin(k\pi/2)}{k\pi/2}=\frac{sinc(k/2)}{2}\)

\[sinc(t)=\frac{sin(\pi t)}{\pi t}\]

# 周期方波频谱c_k=1/2 * sinc(k/2)x_t = np.sort((list(np.arange(-7,10,2))*2))y_t = [1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0]plt.subplot(2,1,1)plt.plot(x_t,y_t)plt.xticks([-4,-2,0,1,2,4],['$T_0$','$-T_0/2$','0','$T_0/4$','$T_0/2$','$T_0$'])plt.yticks([0,1],['0','1'])plt.title('Periodic Square')plt.subplot(2,1,2)x_f = np.arange(-8,9,1)y_f = np.sinc(x_f/2)/2 # spectrumplt.stem(x_f,y_f,use_line_collection=True)plt.title('Corresponding_Spectrum')plt.tight_layout()plt.show()

周期矩形波信号的傅里叶级数\(c_k=\frac{1}{4}{sinc(\frac{k}{4})}\)

# 周期矩形波频谱plt.subplot(2,1,1)x = np.arange(-9,11,2)y_t = [1,1,0,0,0,1,0,0,0,1]plt.plot(x,y_t,drawstyle='steps-pre')plt.title('Rectangular Wave')plt.subplot(2,1,2)x_f = np.arange(-16,17,1)y_f = np.sinc(x_f/4)/4plt.stem(x_f,y_f,use_line_collection=True)plt.title('Rectangular Wave Spectrum')plt.ylim([-0.1,0.3])plt.tight_layout()plt.show()

方波的k=2,4,6分别与矩形波k=4,8,12对齐

k=0对应直流分量，k=1对应基波分量，k=2对应二次谐波

基波频率\(f=1/T_0\), 方波周期使\(T_0\), 矩形波周期是\(2T_0\), 因此同一个k，方波频率是矩形波两倍

即方波的k对应矩形波的2k

因此横轴可理解成频率f或者角频率w

x_f = np.arange(-128,129,1)y_f = np.sinc(x_f/32)/32plt.stem(x_f,y_f,use_line_collection=True)# plt.title('Rectangular Wave Spectrum')plt.ylim([-0.03,0.05])plt.tight_layout()plt.show()

离散谱推广到连续谱

连载67：

当 \(T \rightarrow \infty\), 周期矩形信号将变成非周期矩形信号，谱线间隔将逐渐减小，傅里叶系数将趋近无穷多，频谱幅值也将逐渐减小趋至0

离散谱是线频谱，横轴单位间隔代表基波频率间隔，纵轴代表其复傅里叶系数\(c_k\)

连续谱又称密度频谱，代表单位带宽下的频谱。横轴单位间隔代表基波频率间隔，纵轴代表频谱密度\({c_k}/{\Delta f}\)

# 连载69：周期矩形波离散谱与连续谱比较# plt.suptitle('Left:Discrete Spectrum; Right:Continuoous Spectrum')plt.subplot(3,2,2)x = np.arange(-8,9,1)y_t = [0,-0.05,0,0.05,0,-0.1,0,0.3,0.5,0.3,0,-0.1,0,0.05,0,-0.05,-0.05]plt.plot(x,y_t,drawstyle='steps-post',color='r')# plt.subplots_adjust(hspace=10)plt.title('Square Wave Contiuous Spectrum',fontsize=8)y_f = np.sinc(x/2)/2 # spectrumplt.plot(x,y_f,color='b')plt.subplot(3,2,1)x_f = np.arange(-8,9,1)y_f = np.sinc(x_f/2)/2 # spectrumplt.stem(x_f,y_f,use_line_collection=True)plt.title('Square Wave Discrete Spectrum',fontsize=8)# plt.subplots_adjust(hspace=10)plt.subplot(3,2,4)x = np.arange(-16,17,1)# y_t = [0,-0.05,0,0.05,0,-0.1,0,0.3,0.5,0.3,0,-0.1,0,0.05,0,-0.05,-0.05]y_f = np.sinc(x/4)/2 # spectrumplt.plot(x,y_f,drawstyle='steps-post',color='r')plt.title('Duty-Cycle-25 Rectangular Wave',fontsize=8)plt.plot(x,y_f,color='b')plt.subplot(3,2,3)x_f = np.arange(-16,17,1)y_f = np.sinc(x_f/4)/4 # spectrumplt.stem(x_f,y_f,use_line_collection=True)plt.title('Duty-Cycle-25 Rectangular Wave',fontsize=8)plt.subplot(3,2,6)x = np.arange(-32,33,1)# y_t = [0,-0.05,0,0.05,0,-0.1,0,0.3,0.5,0.3,0,-0.1,0,0.05,0,-0.05,-0.05]y_f = np.sinc(x/8)/2 # spectrumplt.plot(x,y_f,drawstyle='steps-post',color='r')plt.title('Duty-Cycle-12.5 Rectangular Wave',fontsize=8)plt.plot(x,y_f,color='b')plt.subplot(3,2,5)x_f = np.arange(-32,33,1)y_f = np.sinc(x_f/8)/8 # spectrumplt.stem(x_f,y_f,use_line_collection=True)plt.title('Duty-Cycle-12.5 Rectangular Wave',fontsize=8)plt.tight_layout()plt.show()

随着周期T增大，离散谱（左图）谱线间隔减小且谱线幅度渐小

随着周期T增大，连续谱阶梯宽度渐窄，但幅度未变小，其逼近\(X(f)=\frac{T_0}{2}sinc(\frac{T_0}{2}f)\)

令\(\tau=\frac{T_0}{2}\), 则 \(X(f)=\tau sinc(\tau f)\)

由周期矩形信号推广到一般情况(Fourier Transform)：\(X(f)=\int_{-\infty}^{+\infty}x(t)e^{-j2\pi ft}dt\)

由于部分图片显示不出，故贴上备用

各种有用的频谱指标